Rajiv Malhotra Discusses Bharatiya Maths with Jonathan J. Crabtree


| www.twitter.com/rajivmessage | www.twitter.com/jcrabtree |
| www.infinityfoundation.com | www.podometic.in |
THE GREAT MATHS OR MYTHS DEBATE – VIDEO AND TRANSCRIPT
MALHOTRA
Namaste. I’m with an interesting guest Jonathan Crabtree from Australia and we are recording this long-distance. So welcome Jonathan.
CRABTREE
Thank you, Rajiv.
MALHOTRA
Jonathan was introduced to me as somebody who is studying what he calls Bharatiya mathematics. His view is that the mathematics as originally proposed by Indian mathematicians like Aryabhata and some others was not properly imported into Europe.
For instance, they had an aversion to the number zero, and they did not import that properly. So, they distorted it and the mathematics that we have today, modern mathematics is therefore defective.
So welcome to the show Jonathan. Tell us a little about your background, about how you got interested in this and give us an introduction at a very elementary level of your concepts.
CRABTREE
Thank you very much for having me. First of all, I’m greatly honoured to be having this conversation with you. I would say this is the highlight of my mathematical life so far. So, thank you for the honour.
By way of background, I never wanted to be a mathematician or a historian of mathematics. That kind of happened by accident. Really, my curiosity was triggered when I was seven years old in Class 2.
My teacher gave the class an explanation of mathematics that I thought was illogical. What I noticed in 1968 at age 7 was that my teacher had failed to use India’s zero in an explanation of mathematics.
I got very confused by that and then for many years I thought I was a little bit stupid. Because I kept on noticing problems with my teachers’ explanations of elementary mathematics.
So, what happened is, I was studying economics at Melbourne University and I was riding on my way to university and I had an accident in which a truck made an illegal turn. I bounced off the side of the truck and smashed my spine.

I was told by my surgeon that if I moved it was likely that I would never walk again. So, I needed a miracle because my spine was very badly broken. I made it a promise to God that if I could walk again, that I would fix mathematics.
So that was 1983 and so since 1983 until now 37 years, I’ve been working on my personal goal of keeping my promise to God to fix mathematics. So really, my journey started quite by accident, literally.
MALHOTRA
So how did you fix mathematics?
CRABTREE
Well, basically the way that I understand mathematics is very simple. Mathematics is all about relationships between quantities and we count and measure quantities with numbers, very simple.
Now what we know is that all quantities are either zero or greater than zero. For example, if we drive to work, that’s a certain amount of distance. It takes a certain amount of time and the mathematical relationship gives us our average speed.
Or it might be a distance and fuel and we get fuel consumption as the mathematical relationship. So, all mathematics is really about is counts or measures of quantities, and that’s what I’ve started to look at. And really look back into the ancient history of mathematics across many cultures.
MALHOTRA
Tell me one thing, tell us one example, one thing which would be differently treated in Bharatiya Mathematics from Western mathematics. Just give me an example.
CRABTREE
Very simply in Bharatiya Mathematics positives and negatives were simply opposites. And if you have one positive and one negative, they were equal and opposite. And if you were to join them together, they would sum to zero. So, India, Bharat, defined zero by addition of positives and negatives of equal number or magnitude. In the West the way that we’re taught mathematics, we’re told that all negatives are less than positives and yet that’s not how the laws of physics work.
So fundamentally, the ancient Indian mathematics is very symmetrical, and it obeys the laws of physics with zero the most important concept to understand. Yet in the West, the mathematics developed from ancient Greeks that didn’t have 0 and 1 as numbers. So, things became very confused and we needed lots of rules and laws to force the numbers to be correct.
If I were to ask a child “What is greater, a debt of 7 rupees or debt of 4 rupees?”, the child would just say well, “A debt of 7 rupees is a bigger debt than a debt of 4 rupees”. But the English would say that negatives are like debts. They would say that negative 4 is greater than negative 7. That’s a very confusing thing to think about. How can you say a debt of 7 is greater than a debt of 4, but then say that negative 4 is greater than negative 7?
So, there are very simple total differences in, for example, the way that integers are ordered on the number line. With India, we have a symmetric number line where the numbers and the distances are simply equal and opposite. But in the West, we’re taught that just by definition, all negative numbers are less than zero.
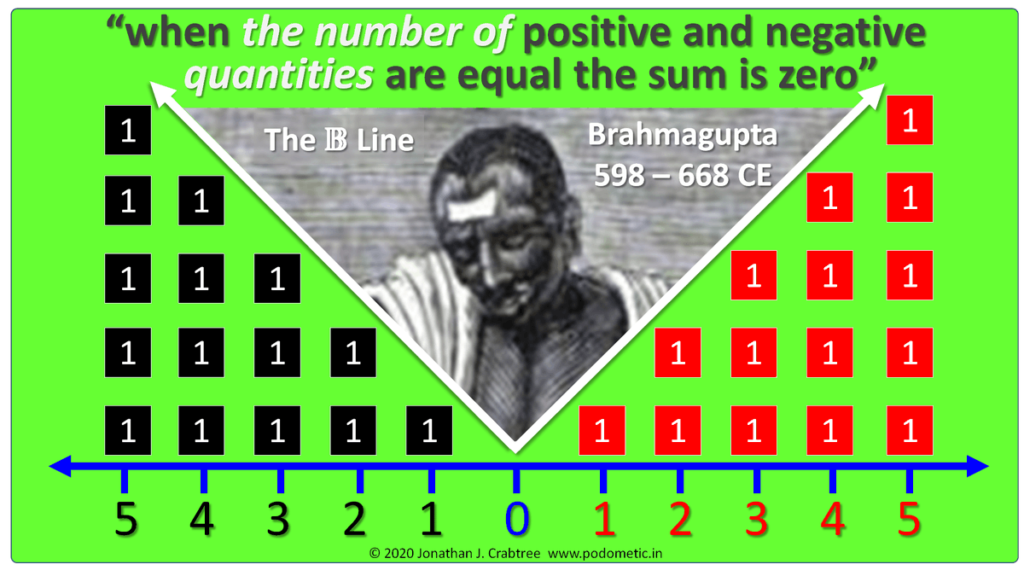
It’s very confusing when you think about zero being the least amount of quantity you can possibly have. Yet negative numbers which represent quantities, somehow those quantities are less than nothing.
It’s impossible in the real world to have any quantity, whether its energy or matter, that’s less than zero. Yet the way that Western mathematics talks about physics and the world, they would have us believe that you can have quantities that are less than zero. But that just simply does not happen in physics.
So, we can very quickly go from the simplest ideas that we might introduce in Class 2 with Integer subtraction. So, if for example, I gave you an example. Often, I ask people in a conference,
“Okay, who can tell me what negative 7 minus negative 4 is?”
Very quickly people get confused because they try and remember the laws of mathematics. And very often people will say,
“Well, I think negative 7 minus negative 4 is negative 11.”
But, if we ask the question the ancient Bharatiya mathematics way, we might say,
“What’s seven negatives minus four negatives?”
Then straight away children would say,
“Three negatives”.
So, there are ways that we talk about mathematics that are totally abstract in Western maths that make no sense. But the ancient way of mathematics was all about describing nouns. So, seven negatives minus four negatives is very simple, three negatives. [Yet] negative seven minus negative four [is] very confusing.
People don’t know what law to apply. So, they try and guess it and they usually guess it wrong is my experience. So very quickly we can, in Class 1, 2 and 3 at school with the ancient way of mathematics. We can introduce negatives and positives at the same time through simple games.
At the moment, children are taught how to count and then maybe another five or six or seven years later, they get introduced to negative numbers, which really makes things very confusing. It’s better to start off with mathematics of positives and negatives and understand how you can multiply them and so on, and things become much much, simpler.
MALHOTRA
With the use of the Indian mathematics Indian integers, what problem can you solve which we cannot solve otherwise? Or is it simply, it’s not the matter of solving other problems, solving more problems differently, but it’s simply a matter of clarity and being able to understand quickly. Is it simply a learning technique that will lead to the same conclusion? Or do you feel that certain problems Indian mathematics can solve which the other one cannot?
CRABTREE
First of all, the way of teaching mathematics the Bharatiya Mathematics way is intuitive and common sense. So, children don’t develop any fear of mathematics straight up. So, everything becomes common sense, even if you subtract a larger number from a smaller number, that’s no problem at all.
So, the logic is correct. The mathematical logic is correct. But then we find that questions like why is negative × into negative a positive also become really clear and simple to understand. Whereas t the moment we have to memorize laws that negative [multiplied] into negative is positive without the intuitive understanding.
As we go through later classes in school, we can then introduce tools like string or rope. We can start to do geometry with rope as well as compass and straightedge. And we can solve geometry problems that are very complicated and almost impossible to solve the old-fashioned way, the Western way. So, for example, squaring the circle is impossible with a compass and straightedge. But it is entirely possible and quite simple to square a circle the shulba sutra way if you use rope.
We actually miss out on a whole lot of understanding about not only numbers but also about geometry when we follow the Western curriculum. That was again developed based on Ancient Greek mathematics, which was out of date by about 1000 years by the time that Brahmagupta was writing his laws of mathematics.
So, in answer to your question, there’s a two-fold improvement. The understanding is there as soon as you introduce positives and negatives in the classroom, which gets rid of the confusion and the fear. And then you find that you have simpler ways of explaining the ideas in mathematics that children find most confusing of all. And they usually involve the ideas of negative numbers. So negative numbers positive numbers are simply equal and opposite and it’s like balancing a seesaw.
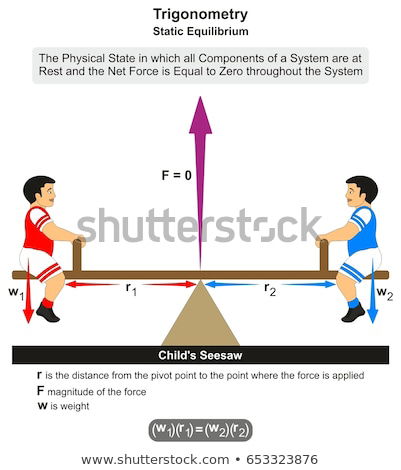
Children can understand how things work in the real world and then straight away they see the real world reflected in the way mathematics is explained in the classroom.
MALHOTRA
Wonderful. So, as you’re familiar, there is a field called philosophy of mathematics. Which is not mathematics itself, but the philosophical premises are what are numbers and so on. Do you feel that the real origin of this has to do with the philosophy of mathematics? In other words, the Indian mathematicians operated from a different philosophical premise on the idea of quantity and the idea of numbers. And therefore, they came up with different techniques or actual tools of the trade. The mechanics of the trade, which you are explaining turned out to be different and simpler and more elegant because they started from a different philosophical premise.
Like there is philosophy of physics. Like there is the study of consciousness, but there is also the philosophy of consciousness. So, there is a field on the philosophy of mathematics.
CRABTREE
Well, I think that you’ve certainly got a very important point that you make there. Because our Western mathematics really originated with ideas of people like Aristotle. And Aristotle had a philosophy in which he would say, for example, that arithmetic that’s basic numbers and geometry, must never ever be connected together. And that’s why if you go through a famous book like Euclid’s [300 BCE] Elements, you don’t find numbers anywhere in Euclid’s elements. When I look at the very oldest Euclid’s Elements. There are no numbers anywhere. The only numbers you’ll find are page numbers if that.
What happened is the ideas of Western mathematics started off with geometry where numbers were disconnected and yet the ancient Indians, they were astronomers. So, the ancient Indians were totally interested in geometry and shapes of planetary movements and quantities of shadow lengths and so on. And they needed to use numbers with their geometry because that’s how astronomy worked for predicting monsoons for planting crops or navigating at sea.
So, the Indians brought number and geometry together and developed a cohesive system where they worked together. But in the Greek way, geometry and numbers were always separate because of the philosophy of Aristotle. Which really then infected the philosophy of mathematics for 2000 years. If we think beyond the philosophy of mathematics, and I will keep this very simple. If we go to number theory, we think about the number theory that developed in the West was all based on, you know, Grassman, Dedekind [and] Peano axioms and so on. They were all based on an idea of number that did not include zero. In fact, many number theorists said that the number one also wasn’t a number.
You had these ideas of successor logic which were lop-sided. All of number theory only developed in the West based on half the number that India had. So western number theory that flowed on from the philosophy was not symmetrical. The Indians had equal and opposite numbers of positives and negatives. But [western] number theory only evolved out of positive counting numbers.
So we’ve got really complicated number theory, that has to make all of these assumptions and prove things in a very convoluted difficult way because they missed out on the simplicity of Brahmagupta’s [628 CE] laws of mathematics, which are totally simpler than any number theory that the West has come up with.
MALHOTRA
So where is this Indian mathematics system being taught, anywhere in the world that you are aware of? Who is teaching this?
CRABTREE
I’m afraid I feel like all alone because I don’t think anybody else really thought there was a problem with mathematics [education]. And I think that because I didn’t have to write a Master’s paper [and] I didn’t have to do a Ph.D., I didn’t have to obey a supervisor at a university telling me how to think and how to style my research. I had total free reign to explore mathematics [for] as long as I wanted in all sorts of directions.
Now, I first came to India by accident. I was talking at a mathematics conference in Hungary back in 2017. And an Indian man, a Professor Santhanam, he saw me speak about Indian mathematics in Hungary. And Dr. Santhanam, he was the President of a mathematics association in India. He said he had never known about the ideas that I was talking about at this conference in Hungary.

So, he invited me to tour India and start explaining India’s own mathematics in his network of schools and I started to talk at conferences in India. And everywhere I go, whether I give lectures at universities in India or mathematics conferences, I just have to explain to the professors there and the teachers there, not just the students but the academics, that this is new research, you will find my papers and my presentations on my website, but this is new research that’s taken me decades literally to assemble. Yet, please just have an open mind and look at the explanations that I present and make up your own mind.
I have many examples of Indian professors of mathematics who totally respect and are delighted with the research that I’ve assembled. And they just simply weren’t aware that there are much simpler ways of explaining mathematics than they’ve been used to and that the world has been following for the last 500 years or so.
Superb lecture. Scholarly and yet easy to follow. I recommend this for parents, students, teachers of history and of math and for anyone interested in India’s ancient history and how India developed mathematical concepts way ahead of the Greeks and of Europe. https://t.co/mzVvkMFP3w
— Dinesh Singh (@DineshSinghEDU) February 10, 2020
So, I think that it’s only really been over the last, probably four years, that I’ve been publishing papers, that the world has started to learn about the difference between the Indian way of mathematics and what’s being currently taught. So my goal is to make all of my presentations all of my videos everything, all my papers free of charge so that everyone can download them read them ,[to] watch the videos and make up their own mind about whether or not the explanations of mathematics make intuitive common sense. www.podometic.in
Also, what did Kousik Sett say…
“By profession I am a mathematics teacher in a school in India. For me life is good for only two things. Learn Mathematics and Teach Mathematics. I must say, today your presentation was beautiful and fascinating. This is the best lecture on elementary and fundamentals of Mathematics I have ever seen. Thanks for giving us such a magnificent, powerful and thought provoking lecture on Indian Mathematics. It has immense importance in terms of originally and to established truth.”
… and what did Abhijit Majumder say?
“It was quite an amazing and mind-boggling experience to get acquainted with the commonplace errors we always make. Your inspirational lecture today is still ringing in my ears.”
And time and time again, people say “Aah! Well, that makes sense. That’s simple”. That’s been a joy for me because it took me over 25 years before I started to really understand mathematics myself. Which sounds crazy, but I’d made that promise in hospital. And so I just stuck at it a very long time.
MALHOTRA
So, Jonathan this is an incredible story, and you have a lot of wisdom to share. I hope the educators in the schools because this has to start at the school level; teaching, mentioning this at the college level is too late.
You have to start with kids at the very elementary level. So I’m hoping that maybe you connect with some of the people who are into very Innovative and very holistic kind of education. There are a lot of people who are at the cutting edge of new ideas of pedagogy and so on, in India.
And maybe offline I can give you some leads and connect you with some people and perhaps you can help them develop a different kind of curriculum.
CRABTREE
Well, that certainly is my goal. I’m aware that NCERT at the moment is looking at revising the curriculum for 2021, and I’m hoping that some of my ideas might find its way into the primary level curriculum for India’s children. I have visited a lot of schools in India and I’ve spoken to children from Class 5 up to Year 12 and a lot of children from Class 5 to Classes 7, 8 and 9 and the children just laugh. The children have fun.
I’m preparing a series of cartoon-style mathematics books in which all of the complicated ideas explained with cartoons. And so the idea is to bring back joy and love and fun and laughter into the classroom as well. So, children, especially understand how amazingly simple and beautiful India’s ancient mathematics is.
So, I certainly agree that it begins at the primary level. And it really begins from Class 1 on and if people go to my website, they’ll see I’ve already got some information specifically for Class 1 which is based on the current curriculum in India and between now and about a year’s time, I’ll be releasing year-by-year eBooks that explain level by level how to explain the Indian way of mathematics that’s consistent with the Indian curriculum.
So my goal is not to force change but to simply provide information alongside the formal books that are taught in schools to say. Well here are some other ways of explaining the mathematical ideas as well, that teachers can use as a supplementary text. So, I’m trying to make it as simple as possible for the education ministers to have a really good honest look at the ideas that I’ve assembled.
And really, it’s important for me to honour the Indians like Aryabhata Bhaskara and Brahmagupta because what I’m really doing is just bringing back their own mathematical writings. I’ve invented many new ways of sharing the information and presenting it, but really all credit has to go back to India’s original astronomers and mathematicians who documented this information.
But as you mentioned in your introduction, unfortunately, India’s zero and the symmetric ideas of positive and negative quantities got lost before there were understood in the Arabic world. And because the Arabic world then introduced what they thought was Hindu mathematics to Europe, Europe never really understood Indian mathematics.

So my goal is simply to advocate for Aryabhata and Brahmagupta and Bhaskara and many other Indians, who had very simple ideas. I’m just hoping to bring those ideas of those mathematical geniuses to life in fun ways so that children can appreciate their own mathematical Superstars
At the moment, everyone in India barracks for the Indian cricket team. But when it comes to mathematics, everyone has to obey the British cricket team, the English cricket team. Well I’m saying we barrack for India in mathematics as well as in cricket.
MALHOTRA
Wonderful. Well, thank you very much. All the best to you and let’s stay in touch. Namaste.
CRABTREE
Ok. Thank you very much. Thank you. Thank you, Rajiv.
DISCLAIMER: The author is solely responsible for the views expressed in this article. The author carries the responsibility for citing and/or licensing of images utilized within the text.
